Co to jest cosinus 180 stopni?
Cosinus kątowi 180 stopni przypisuje wartość −1, co oznacza, że na osi poziomej znajduje się po stronie ujemnej, tuż obok jedynki trygonometrycznej w układzie współrzędnych. Ten kąt wprowadza nas w świat funkcji trygonometrycznych, ponieważ pełni fundamentalną rolę w wyprowadzaniu wzorów redukcyjnych oraz w badaniu symetrii i okresowości funkcji cosinus.
Zrozumienie wartości cosinusa dla 180° jest niezwykle ważne, zwłaszcza gdy analizujemy zachowanie tych funkcji na okręgu jednostkowym. Ciekawie jest zauważyć, że im głębiej się zagłębiamy w temat trigonometrów, tym bardziej ta konkretna liczba staje się przydatna zarówno w praktycznych zastosowaniach, jak i w bardziej teoretycznych koncepcjach.
Jaką wartość ma cosinus 180 stopni?
Wartość cosinusa dla kąta wynoszącego 180 stopni to -1. Oznacza to, że cosinus 180° przyjmuje dokładnie tę wartość. Na okręgu jednostkowym, punkt przypisany temu kątowi ma współrzędną x równą -1, co skutkuje tym, że cosinus jest ujemny.
Ta wartość jest istotna i regularnie wykorzystuje się ją w:
- analizie funkcji trygonometrycznych,
- obliczeniach opartych na wzorach redukcyjnych.
Cosinus 180° stanowi jedną z podstawowych wartości w kontekście funkcji trygonometrycznych.
Jak obliczyć cosinus 180 stopni z tabeli wartości trygonometrycznych?
Obliczając cosinus kąta wynoszącego 180 stopni, warto skorzystać z dostępnych tabel wartości trygonometrycznych. Wystarczy znaleźć odpowiednią pozycję z kątem 180° i odczytać przypisaną mu wartość funkcji cosinus. Wartości dla popularnych kątów są zazwyczaj podane z dużą precyzją, a w przypadku kąta 180° cosinus wynosi −1.
Tego typu tabele znacznie ułatwiają szybkie i trafne sprawdzenie wartości cosinusa. Dzięki nim unikamy skomplikowanych obliczeń i nie musimy sięgać po wzory. Prosto i szybko potwierdzamy, że cosinus kąta 180° to −1.
Jak cosinus 180 stopni występuje na okręgu jednostkowym?
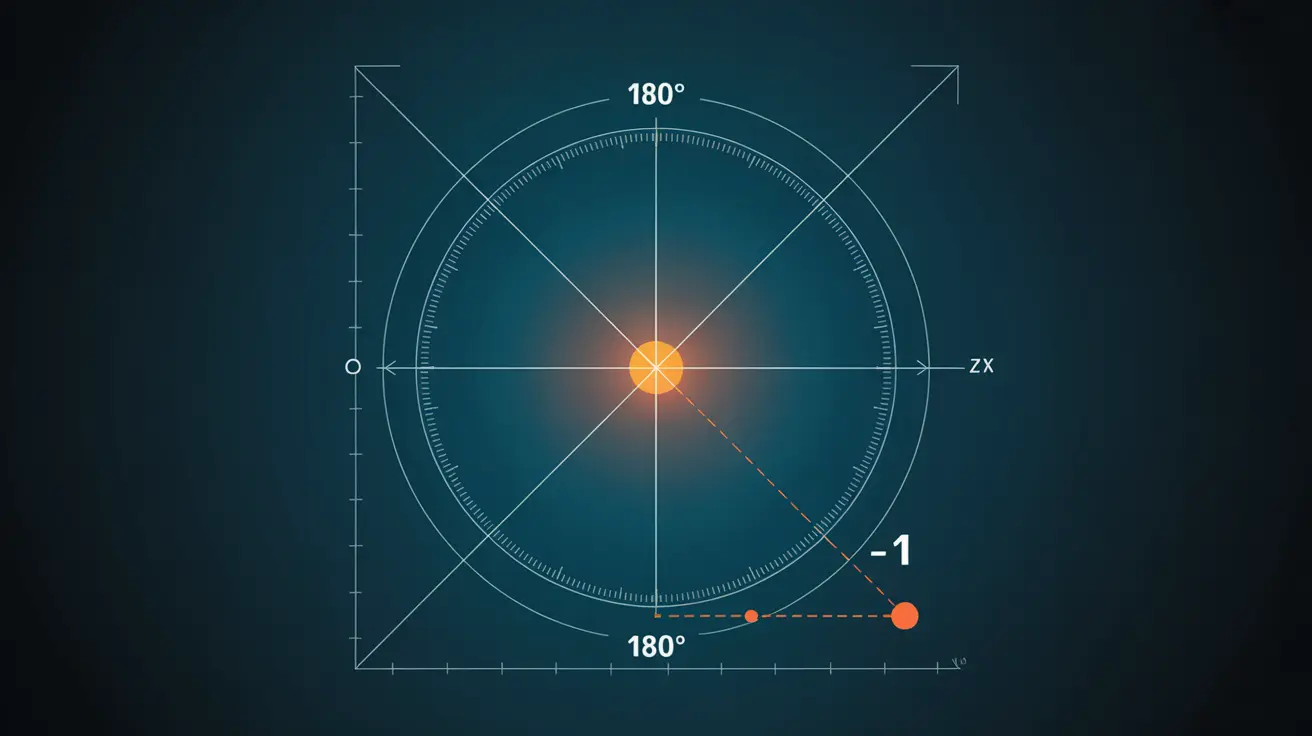
Na okręgu jednostkowym wartość cosinusa dla kąta 180 stopni odpowiada współrzędnej x punktu, który znajduje się po lewej stronie środka układu współrzędnych. Ten specyficzny punkt ma współrzędne (-1, 0). Kąt 180° wyznaczany jest od osi x, w kierunku przeciwnym do ruchu wskazówek zegara. W związku z tym, cosinus kąta 180° wynosi -1, co również jest odzwierciedleniem odciętej tego punktu.
Z kolei sinus tego kąta wynosi 0, co dotyczy rzędnej na okręgu. Wartość cosinusa ilustruje przesunięcie w lewo wzdłuż osi poziomej w odniesieniu do środka okręgu jednostkowego. To ważny aspekt wizualizacji funkcji trygonometrycznych. Ostatecznie, cosinus kąta 180 stopni ukazuje położenie punktu o współrzędnej x = -1 na okręgu jednostkowym, co podkreśla istotność tej funkcji dla kąta 180°.
Jakie są wzory redukcyjne dla kąta 180°?
Wzory redukcyjne dla kąta 180° pozwalają na przekształcenie wartości funkcji trygonometrycznych kątów w formie 180° ± α, co opiera się na kącie α. Przy kosinusie mamy do czynienia z następującymi równaniami:
- cos(180° − α) = −cos α,
- cos(180° + α) = −cos α.
Wynika stąd, że kosinus kąta oddalonego od 180° o kąt α ma wartość przeciwną do kosinusa samego kąta α.
Podobne zasady odnoszą się do funkcji sinus:
- sin(180° − α) = sin α,
- sin(180° + α) = −sin α.
Zakres wartości tangensa i cotangensa również podlega tym regułom:
- tg(180° − α) = −tg α,
- tg(180° + α) = tg α,
- ctg(180° − α) = −ctg α,
- ctg(180° + α) = ctg α.
Te wzory wynikają z symetrii funkcji trygonometrycznych i znacznie ułatwiają przeprowadzanie obliczeń. Dzięki nim możliwe jest łatwiejsze rozwiązywanie równań dotyczących kątów w pobliżu 180°.
Zastosowanie tych wzorów przyspiesza proces przekształcania oraz analizy funkcji sinus, kosinus, tangens i cotangens związanych z kątami bliskimi 180°. To ma kluczowe znaczenie w obszarze matematyki i fizyki.
cos(180° − α): wzór i przykłady
Wzór na cosinus kąta pomniejszonego o α, czyli cos(180° − α), można zapisać jako: cos(180° − α) = −cos α. Oznacza to, że wartość cosinusa kąta, który wynosi 180° minus α, jest równa przeciwną wartością cosinusa kąta α.
Na przykład, jeśli posiadamy wartość cos α równą 0,5, wówczas obliczamy cos(180° − α) jako −0,5. Taki wzór staje się niezwykle pomocny, ponieważ umożliwia sprawniejsze obliczenia wartości funkcji trygonometrycznych oraz rozwiązywanie zadań z wykorzystaniem cosinusa. Zjawisko to wynika z symetrii funkcji cosinus na kole trygonometrycznym w stosunku do osi pionowej.
Przyjrzyjmy się kilku konkretnym przykładowi:
- dla α = 60°: cos(180° − 60°) = −cos 60° = −0,5,
- dla α = 45°: cos(180° − 45°) = −cos 45° ≈ −0,707.
Dzięki temu wzorowi łatwo można obliczać wartości cosinusa dla kątów większych niż 90°.
cos(180° + α): wzór i przykłady
Wzór \( \cos(180° + \alpha) = -\cos \alpha \) pokazuje, że gdy dodamy 180° do kąta \( \alpha \), wartość cosinusa zmienia swój znak. Tak więc, cosinus kąta o 180° większego od \( \alpha \) jest przeciwny do cosinusa kąta \( \alpha \). Ta zmiana jest efektem symetrii oraz okresowości funkcji cosinus.
Na przykład, jeżeli mamy \( \cos \alpha = 0,7 \), to w rezultacie otrzymujemy \( \cos(180° + \alpha) = -0,7 \). Takie wzory redukcyjne są niezwykle przydatne, ponieważ:
- upraszczają obliczenia,
- ułatwiają analizę funkcji trygonometrycznych,
- pomagają w lepszym zrozumieniu ich właściwości.
Jak okresowość funkcji cosinus wpływa na wartość dla kąta 180°?
Funkcja cosinus charakteryzuje się okresem wynoszącym 360°, co oznacza, że za każdym razem, gdy dokonujemy pełnego obrotu koła, jej wartość się powtarza. Dla kąta 180° cosinus przyjmuje wartość -1. Ta okresowość jest ważna, ponieważ dzięki niej mamy do czynienia z równaniami, które można uprościć; dla każdego kąta 180° + k·360°, gdzie k jest liczbą całkowitą, wynik będzie taki sam: cos(180°) = cos(180° + 360°·k) = -1.
Dzięki tym właściwościom możemy łatwo przewidywać wartości cosinusa również dla kątów większych niż 360°. Takie podejście ułatwia rozwiązanie równań trygonometrycznych z udziałem tej funkcji. Okresowość sprawia, że wartości cosinusa, które znajdujemy w punktach oddalonych o wielokrotności 360°, pozostają niezmienne, co jest niezwykle istotne w analizie funkcji oraz interpretacji jej wykresów.
Jak cosinus 180 stopni porównuje się z wartościami sinusa, tangensa i cotangensa dla tego kąta?
Dla kąta 180° cosinus osiąga wartość -1, co oznacza, że wskazuje on maksymalną wartość ujemną na osi poziomej w okręgu jednostkowym. Sinus tego kąta to 0, a punkt odpowiadający kątowi 180° znajduje się bezpośrednio na osi x.
Sytuacja z tangensem jest podobna, ponieważ jego wartość także wynosi 0. Takie wyniki wynikają z faktu, że tangens to stosunek sinusa (0) do cosinusa (-1). W przypadku cotangensa sprawa jest bardziej skomplikowana — jego wartość jest nieokreślona lub dąży do nieskończoności. Dlaczego tak się dzieje? Ponieważ cotangens oblicza się jako iloraz cosinusa (-1) do sinusa (0), a, jak wiadomo, sinus nie może być równy 0.
Te różnorodne wartości jasno ukazują, że cosinus kąta 180° znacząco różni się od sinusa, tangensa oraz cotangensa zarówno pod względem znaku, jak i istnienia tych wartości. To właśnie te różnice odgrywają kluczową rolę w analizie funkcji trygonometrycznych.
Jak wykorzystać cosinus 180 stopni w zadaniach z funkcji trygonometrycznych?
Cosinus 180 stopni odgrywa fundamentalną rolę w kontekście funkcji trygonometrycznych, ponieważ jego wartość wynosi -1. Ta charakterystyka umożliwia szybkie uproszczenie równań oraz skomplikowanych obliczeń, zwłaszcza w odniesieniu do kątów w formie 180° ± α.
Wartość ta jest istotna w kontekście wzorów redukcyjnych, które pomagają w przekształcaniu kątów większych niż 90° na ostre, co znacząco przyspiesza proces obliczeń. Co więcej, cosinus 180° jest pomocny w badaniach nad symetrią funkcji trygonometrycznych:
- funkcja ta jest parzysta,
- funkcja ta jest okresowa,
- powraca co 360°.
W zastosowaniach geometrycznych i fizycznych, ta konkretna wartość staje się narzędziem do ustalania pozycji punktów na okręgu jednostkowym. Dodatkowo, ułatwia ona manipulację wyrażeniami w równaniach analitycznych. W związku z tym, posługiwanie się cosinusem 180° jest niezbędne w rozwiązywaniu równań, analizie wykresów oraz określaniu wartości funkcji trygonometrycznych.
Jak cosinus 180 stopni reprezentuje się na wykresie funkcji trygonometrycznej?
Na wykresie funkcji trygonometrycznej, cosinus osiąga interesujący moment w punkcie odpowiadającym kątowi 180 stopni, który ma współrzędne (180°, -1). Oś pozioma przedstawia kąt wyrażony w stopniach, natomiast oś pionowa wskazuje wartość funkcji. Ten punkt stanowi minimum na wykresie funkcji cosinus, ponieważ dla kąta 180 stopni wartość cosinusa wynosi dokładnie -1.
To właśnie ta lokalizacja wyróżnia się jako najniższy punkt fali okresowej, co ma istotny wpływ na jej kształt oraz symetrię.
Ta unikalna wartość jest niezbędna do głębszego zrozumienia funkcji trygonometrycznych oraz dostrzegania ich cykliczności.
Dlaczego miara kąta 180 stopni jest istotna w trygonometrii?
Miara kąta 180 stopni odgrywa kluczową rolę w trygonometrii. Reprezentuje ona półpełny obrót na kole jednostkowym, co stanowi fundament analizy funkcji trygonometrycznych. Kąt ten funkcjonuje jako punkt odniesienia dla takich funkcji, jak cosinus, sinus czy tangens.
Zrozumienie kąta 180° otwiera drzwi do zastosowania wzorów redukcyjnych, które znacząco upraszczają obliczenia. Dzięki tym wzorom jesteśmy w stanie ustalić wartości funkcji dla kątów poza zakresem kątów ostrych.
Ponadto, kąt 180 stopni jest kluczowy w badaniu:
- symetrii funkcji trygonometrycznych,
- okresowości funkcji,
- przekształcaniu między układami miar: stopniami a radianami.
Ta miara ułatwia dodatkowo rozwiązywanie równań i zadań geometrycznych, co jest podstawą w analizie matematycznej i geometrii.
Kąt 180° jest nie tylko teoretycznym konceptem, ale również praktycznym narzędziem w aplikacjach trygonometrycznych.
W jakiej jednostce można przedstawić kąt 180 stopni: stopnie i radiany
Kąt o wielkości 180 stopni można opisać w dwóch głównych jednostkach: stopniach i radianach. W systemie stopniowym ten kąt prezentuje się jako 180°, co jest łatwe do uchwycenia i powszechnie stosowane. Z kolei w miarze łukowej, która znajduje zastosowanie w matematyce oraz trygonometrii, wartość 180° odpowiada π radianom.
Liczba π, znana jako pi, to fundamentalna stała matematyczna, która definiuje stosunek obwodu koła do jego średnicy, przyjmując wartość około 3,14159. Aby przeliczyć stopnie na radiany, możemy skorzystać z prostego wzoru:
- 180° to równoznaczne π radianów.
Zrozumienie tej zależności ma kluczowe znaczenie w kontekście funkcji trygonometrycznych. Na przykład, jest to istotne przy analizie okresowości tych funkcji oraz ich wartości na kole jednostkowym. Co więcej, zastosowanie radianów upraszcza obliczenia i ułatwia wykorzystywanie wzorów w różnych obszarach matematyki oraz fizyki.