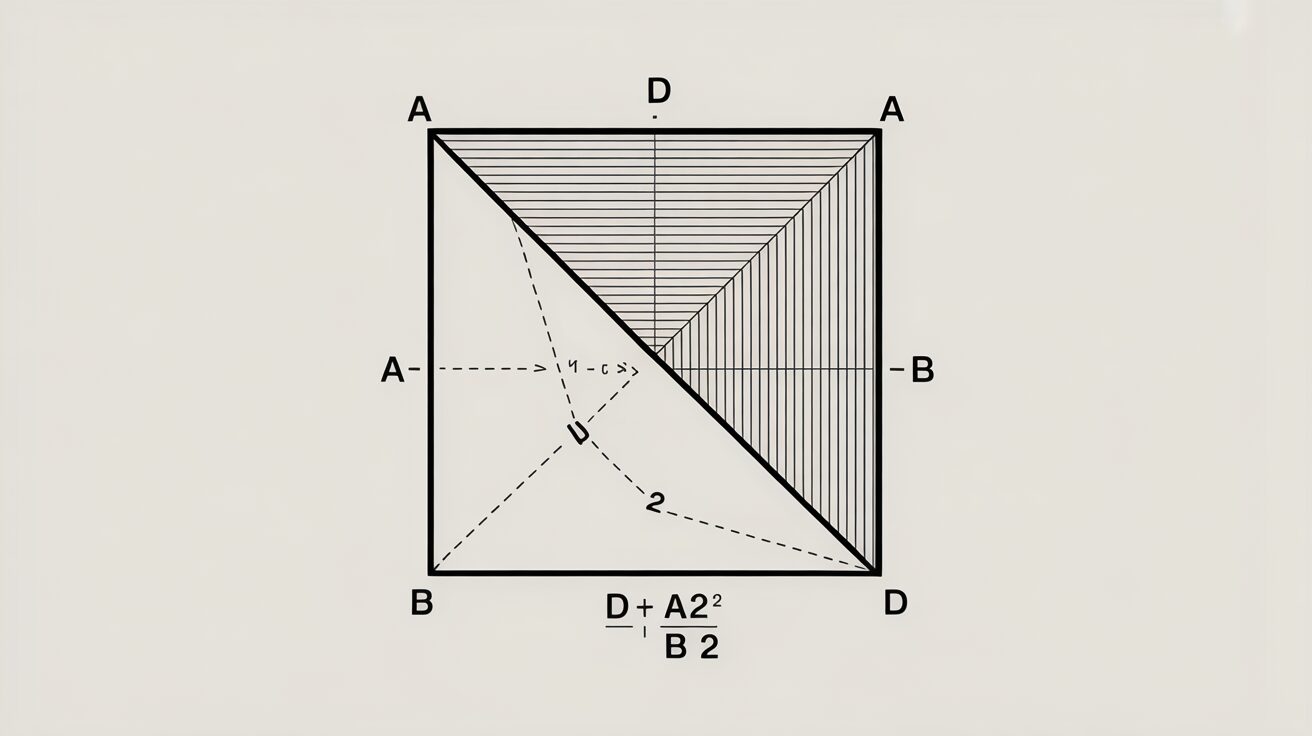
Jaki jest wzór na przekątną prostokąta?
Formuła na obliczenie przekątnej prostokąta to d = √(l² + w²), w której d oznacza długość przekątnej, l to długość, a w szerokość prostokąta. Wywodzi się ona z twierdzenia Pitagorasa. Twierdzenie to stwierdza, że w trójkącie prostokątnym kwadrat przeciwprostokątnej jest równy sumie kwadratów dwóch pozostałych boków. W przypadku prostokąta, przekątna pełni rolę przeciwprostokątnej w trójkącie utworzonym przez dwa jego boki oraz samą przekątną.
- dzięki tej formule możemy szybko wyznaczyć długość przekątnej prostokąta, mając dane jego długość i szerokość,
- jest ona powszechnie stosowana w geometrii przy rozwiązywaniu problemów związanych z wymiarowaniem przestrzeni,
- dodatkowo jest niezwykle przydatna podczas projektowania konstrukcji architektonicznych i inżynieryjnych.
Wzór na długość przekątnej prostokąta
Aby obliczyć długość przekątnej prostokąta, stosujemy wzór d = √(a² + b²), gdzie a oznacza długość, a b szerokość tego kształtu. Wzór ten opiera się na twierdzeniu Pitagorasa. Zgodnie z nim, w trójkącie prostokątnym suma kwadratów przyprostokątnych jest równa kwadratowi przeciwprostokątnej. W kontekście prostokąta to właśnie przekątna pełni rolę tej przeciwprostokątnej.
Zastosowanie twierdzenia Pitagorasa
Twierdzenie Pitagorasa odgrywa kluczową rolę w geometrii, zwłaszcza gdy zachodzi potrzeba obliczenia długości przekątnej prostokąta. Dzielimy prostokąt na dwa identyczne trójkąty prostokątne, gdzie boki prostokąta stanowią przyprostokątne tych figur, a przekątna pełni rolę przeciwprostokątnej. To twierdzenie umożliwia nam stwierdzenie, że suma kwadratów długości boków (l i w) odpowiada kwadratowi długości przekątnej (d). Dzięki wzorowi d = √(l² + w²) można precyzyjnie określić wartość d. Takie obliczenia są nieocenione w dziedzinach takich jak budownictwo czy architektura, gdzie dokładność pomiarów jest niezwykle istotna.
Przekątne prostokąta – wzór
Przekątną prostokąta wyznaczamy za pomocą wzoru: d = √(a² + b²), gdzie a oraz b reprezentują długości boków. Ten wzór opiera się na twierdzeniu Pitagorasa, które mówi, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi przeciwprostokątnej. Przekątna prostokąta tworzy taki właśnie trójkąt z bokami figury i stanowi najdłuższą linię w tej formie. Dzięki znajomości wymiarów boków, możemy ją łatwo obliczyć.
Wyrażenie wzoru: d = √(a² + b²)
Wzór d = √(a² + b²) służy do obliczenia długości przekątnej w prostokącie. W tym równaniu d jest długością przekątnej, natomiast a oraz b reprezentują długości boków prostokąta. To doskonały przykład zastosowania twierdzenia Pitagorasa.
Przekątna razem z bokami tworzy trójkąt prostokątny, gdzie boki są przyprostokątnymi. Dzięki temu wzorowi można w prosty sposób określić długość przekątnej, mając dane wymiary boków figury.
Jak znaleźć przekątną prostokąta znając długości boków?
Aby znaleźć przekątną prostokąta, gdy dysponujemy długościami jego boków, oznaczmy je jako a i b.
Postępuj zgodnie z poniższymi krokami:
- Podnieś te wartości do kwadratu: \(a^2\) i \(b^2\),
- dodaj te kwadraty, wykonując sumę: \(a^2 + b^2\),
- wystarczy wyciągnąć pierwiastek kwadratowy z otrzymanej sumy, aby ustalić długość przekątnej.
To podejście opiera się na Twierdzeniu Pitagorasa, które wykorzystuje się w kontekście trójkąta prostokątnego tworzonego przez boki oraz przekątną figury. Wzór ten przyjmuje postać: \(d = \sqrt{a^2 + b^2}\).
Przykładowo, mając bok a o długości 3 m oraz bok b mierzący 4 m, obliczamy przekątną jako:
\(\sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\) m.
Oznaczenie boków prostokąta jako a i b
Podczas obliczeń związanych z prostokątem, standardowo przyjmujemy oznaczenia `a` dla długości oraz `b` dla szerokości. Takie przypisanie ułatwia zastosowanie matematycznych wzorów, zwłaszcza gdy chcemy określić długość przekątnej tej figury.
Podnoszenie długości boków do kwadratu
Podnoszenie długości boków do kwadratu to kluczowy etap w obliczaniu przekątnej prostokąta. Oznacza, że musimy podnieść wartości a oraz b, czyli długości boków, do kwadratu. W efekcie uzyskujemy a² i b². Te liczby są konieczne do dalszych obliczeń związanych z przekątną.
Dodawanie podniesionych wartości
Podniesienie wartości do kwadratu stanowi kluczowy etap w obliczaniu przekątnej prostokąta.
- podnosimy do kwadratu długości boków, które oznaczymy jako a i b, co daje nam wyniki a² oraz b²,
- potem te wartości sumujemy: a² + b²,
- ta suma stanowi podstawę dla dalszych operacji prowadzących do ustalenia długości przekątnej,
- w tym momencie niezbędne jest przejście do kolejnego kroku,
- czyli wyciągnięcia pierwiastka kwadratowego z uzyskanej sumy kwadratów.
Obliczanie pierwiastka z sumy kwadratów
Aby znaleźć długość przekątnej prostokąta:
- zaczynamy od dodania kwadratów długości jego boków,
- następnie z tej sumy wyciągamy pierwiastek kwadratowy.
Przykładowo, gdy boki mają długości 3 i 4:
- obliczamy \(3² + 4²\),
- co daje \(9 + 16 = 25\),
- pierwiastek kwadratowy z tej liczby to \(\sqrt{25} = 5\),
- co oznacza, że przekątna mierzy 5 jednostek.
Przykład obliczenia przekątnej prostokąta
Aby dowiedzieć się, jak obliczyć przekątną prostokąta, przyjrzyjmy się przykładowym wymiarom:
- l = 3,
- w = 4.
Następnie wykonujemy obliczenia:
- Podnosimy każdą z długości do kwadratu: \( 3² = 9 \) oraz \( 4² = 16 \),
- Sumujemy te wartości: \( 9 + 16 = 25 \),
- Wyciągamy pierwiastek kwadratowy z otrzymanej sumy, co prowadzi nas do wyniku: \( d = √25 \), a więc \( d = 5 \).
W efekcie, przekątna prostokąta o bokach długości 3 i 4 mierzy dokładnie 5 jednostek.
Przykładowe wartości długości boków
Przykładowe wymiary boków prostokąta to l = 3 oraz w = 4. Aby znaleźć długość przekątnej, można zastosować twierdzenie Pitagorasa. Wzór na przekątną wyraża się jako: \( d = \sqrt{a^2 + b^2} \).
W przypadku tych wymiarów obliczenia wyglądają następująco:
- \( d = \sqrt{3^2 + 4^2} \),
- \( d = \sqrt{9 + 16} \),
- \( d = \sqrt{25} = 5 \).
A więc przekątna prostokąta z bokami o długościach 3 i 4 to dokładnie 5 jednostek.
Krok po kroku: Obliczanie przekątnej
Aby obliczyć przekątną prostokąta, wykonaj następujące kroki:
- określ długości boków prostokąta: l i w,
- podnieś te liczby do kwadratu, co da ci l² oraz w²,
- zsumuj otrzymane wartości: l² + w²,
- wyciągnij pierwiastek kwadratowy z tej sumy, aby uzyskać długość przekątnej: d = √(l² + w²).
Ten proces opiera się na podstawowych działaniach matematycznych oraz twierdzeniu Pitagorasa, które są niezbędne do dokładnego określenia długości przekątnej każdego prostokąta.